Dynamic Energy Analysis of the Indian Nuclear Power Programme
Dynamic Energy Analysis of the Indian Nuclear Power Programme
By R. Ashok Kumar,B.E.,M.E., Negentropist, Bombay Sarvodaya Mandal, 299,Tardeo Road, Nana Chowk, Mumbai-400007.
E-mail: rakumra@yahoo.com
29 November 2004
© 2017 Ramaswami Ashok Kumar
http://enenews.com/nuclear-expert-it-is-not-advisable-to-eat-bluefin-tuna-radiation-deposited-over-600000-sq-miles-of-pacific-cesium-crosses-placental-barrier-of-animals
When the energy audit is negative, the risks are adversely high leading to extinction level events.
It is absolutely essential to reexamine the Indian Nuclear Energy Programme in the light of its adverse energy audit. Here an audit of 1000 MW nuclear power plants is performed with the plan of having 24000 MW stabilised on line by 2025 AD. It is envisaged by Dr MR Srinivasan, former AEC Chair, who wrote recently in the Hindu on the Indian Nuclear Power Scenario, that some 200,000 MW Capacity of an assortment of nuclear plants shall be on line by 2050 AD.
The analysis shows that even a quarter of a century later, by 2025 AD, no nuclear power will be available to society. In fact the Nuclear programme will be still paying back the energy consumed by the nuclear industry, by the time one set of 2 x 1000 MW nuclear reactors are decommissioned in 2025! See Table 1 and Figures 1 and 2 below: One would have thought that as fresh nuclear capacity is added, it would meet the shortage of power demand. In reality, it is never so(Figure 1).Of course, if the government is serious about the decommissioning, it must have energy for this as well, for a century or more. Also, waste management has become lethally serious: In a nation which is aware of the implications, it is worthwhile to note that even after more than half a century, the USA had to find itself in the unenviable position of having to take care of wastes at Yucca mountain site by designing the repository, not for 10,000 years as the Environmental Protection Agency, USA, wanted, but for 300,000 years or more before groundwater radiation exceeded drinking water limits at the boundary of the site as required by scientists at the National academy of Sciences: That practically means : one should be transscientific! Or abandon nuclear power, and the existing sites for storage beside nuke power stations should continue. See court ruling of July 9,2004 at the URL:
http://pacer.cadc.uscourts.gov/docs/common/opinions/200407/01-1258a.pdf
This article also contains an electronic reproduction of a net energy analysis of the Indian Nuclear Programme as it was envisaged for 1985-2001. This appeared in the PPST Bulletin, No.18,March 1989,pp 10-25. This includes details of construction energy inputs and waste storage inputs used for the analysis. This gives an idea of the output/input ratios of Pressurised Heavy Water Reactors used in India.. In this article waste storage energy debits are included in the dynamic energy analysis. This is because of the extremely slowly deployable nature of the nuclear programme as shown above. This makes the time constant of transients(growth) the same order as the lifetime of the programmes, of interim above ground waste storages, and as the reactors are decommissioned, the need for the programme growth at some constant rate to prolong, albeit, absolutely serving no net energy production purpose except to conspiciously consume finances, energy and power with disastrous consequences to life.
As pointed out before, the Japanese Nuclear Energy Programme and the French are equally adverse regarding the energy audit, as negative as the USA’s.
References:
On Energy Audit of Nuclear Fuel Cycles:
energy audit of nuclear fuel cycles
at http://energyauditofnuclearfuelcycles.blogspot.in/
On health effects of n-power:
http://isisunveiledhenp.blogspot.com/2010/07/health-effects-of-nuclear-power-during.html
http://plutoniumaradiumabillionpeoplehitdna.blogspot.com/
On dual use of n-power byproducts:
http://frozenevolutionofmind.blogspot.com/
or
http://isisunveiled.rediffblogs.com
On the cumulative and synergistic effects of modern civilisation:
Nuclear Fundamentalism
http://nuclearfunda.blogspot.com/
INDIAN NUCLEAR ENERGY PROGRAMME: AN ENERGY AUDIT: NUCLEAR INDUSTRY DEMAND AND CAPACITY BUILD UP:1998-2025(Table 1: Please right click on the blackness and put on separate tab, right click on the black image in the separate tab, then click on image info to view the table!)


Figure 1:(Click on the figure to view) Nuclear Capacity Build Up requires that Nuclear Industry Demand be met by thermal power, exacerbating the greenhouse effect substantially, in perpetuity. This is so, even after 2025 as the adverse energy audit goes on and on as the Nuclear Growth continues, in fact many decades more than the life- time of a nuclear reactor.
INDIAN NUCLEAR ENERGY PROGRAMME: AN ENERGY AUDIT(Click to view Figure 2)
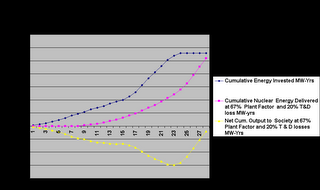
Figure 2: The Indian Nuclear Energy Programme is an enormous consumer of high quality energy. As shown, there is no net energy output available to society even 28 years into the programme,assumed to have commenced from 1998. Since the aim is to go ahead with nuclear power even after 2025 when 200000 MW are proposed to be put on line by 2050, the programme will be a perpetual consumer of energy from society, rather than giving any net output.
The paper The Indian Nuclear Energy Programme- A Net Energy Analysis originally published in the PPST Bulletin referred to in the above article follows.
PPST Bulletin, No. 18, March 1989.
The Indian Nuclear Energy Programme- A Net Energy Analysis
By R. Ashok Kumar, B.E.,M.E(Power),Negentropist, Bombay Sarvodaya Mandal, 299, Tardeo Road, Nana Chowk, Mumbai-400007.
E-mail: rakumra@yahoo.com
The article performs an energy audit of the Indian Nuclear Energy Programme over the period 1985-2001. It demonstrates that the annual ratio of output/input over this period is low, thus adversely affecting the net energy output of the programme. This programme is critically dependent on untested methods of disposal of hazardous wastes. Such methods demand a high-volume investment in energy, lasting over several decades, to keep them isolated, which further reduces the efficacy of the nuclear programme.
One of the key conclusions of this study is that the Nuclear Energy Programme consumes so to speak, five times the energy that it is projected to deliver. Such a conclusion is particularly applicable for 1000 MW plant-sizes. The ultimate production pf nuclear energy/electricity comes after 15 years, but, in order to construct, maintain the plants and stabilise the waste disposal system, five times that much energy, in the form of precious fossil fuels are used up, contributing to the melting of the glaciers. Thus it is energetically unfavourable. Worse still, it is unfavourable in monetary terms too, for the electricity produced will be ten times costlier. This after investing an extraordinary volume of energy and money to the tune of Rs. 20,000 Cr(1985 Rupees)(for 10050 MW installed capacity).
It thus seems the Nuclear Energy Programme is designed to fritter away scarce energy resources and capital that will pay less and cost more. Coupled with this is the additional fact that the waste disposal systems involved are untested and even speculative. A plea is made herein to halt immediately the effort wasted on an immature energy conversion technology aas the Nuclear Energy Programme in India.
Introduction
In any large scale programme of installation of thousands of crore of rupees worth of electricity-generating stations, year after year, it is very essential that we first examine
-whether the programme supplies more, in fact much more energy than it consumes in its construction, operation and maintenance;
-how complete the technology is; that is, whether its by-products can be used or absorbed by nature in such a way that nothing is ever wasted;
-to what extent it affects the health of the environment, including all life.
When such a series of exercises were carried out in various parts of the world, it was noticed that nuclear fission technology is immature and not ready for deployment where life exists. We have so evolved that the ecological base assures health, provided we harmonise our behaviour with the rest of all that is. That is why nuclear energy is actively driving the life patterns on this globeby optimally situating itself in the sun 150 million kilometers away. Careful analysis shows that the problem of safety of artificial nuclear power is insoluble. In fact energy audit studies show that without an economical and safe method of disposal of wastes generated by fission technology, the nuclear programme would always be a net consumer of energy. And it was also found, after the most careful of deliberations, that there is no solution at all to the waste disposal problem. Radioactivity should not be created by man in the first place.
Thus, many states in the U.S.A have prohibited the exercise of the nuclear energy option by legislation, unless satisfactorily demonstrated methods of waste disposal are economically and safely possible for all times. Also the market forces inthe US seem to work against adoption of nuclear power. But, most important, the public are becoming extremely vigilant. Still there is the other side and America possesses 75000 MW of the most dangerous nuclear reactors in operation and the commitment is for a total upwards of 100,000 MW. However many of these have been shutdown indefinitely, although the number of those shutdown is not exactly known. Sweden with 9400 MW of nuclear power, has adopted a policy of phasing out nuclear power by 2010 AD. Austria and Philippines have renounced the nuclear option. In Soviet Russia the citizens have protested against the setting up of a nuclear plant at Krasnodar. In Kaiga, in India, people are up against changing their life styles by buying the dangers of nuclear power. The people of Kerala successfully refused a nuclear plant at Peringome.
Since a clear cut energy audit is not readily available for the Indian Nuclear Programme, this article examines the Indian programme by carrying out an energy audit for the period 1985-2001 AD, with the help of available Indian and foreign data. On account of the nature of the problem, safety aspects cannot but be taken into account in the analysis. The capital, construction, operation, maintenance and waste management costs of nuclear plants have escalated considerably since the Three Mile Island and Chernobyl disasters. In view of this, there is an urgent need for a thorough reassessment of the entire nuclear power generation programme. This article purports to highlight the energy aspects of the programme so that an informed debate can be initiated.
The Indian Nuclear Power Programme envisages the construction of Candu type nuclear reactors; the plan is to have a total installed capacity of 10,050 MW by 2001 AD. Candu reactors are the Canadian deuterium-uranium type reactors- heavy water- moderated heavy water-cooled and natural uranium fuelled . We extend the methodology of Lovins and Price(1975) so as to be applicable to the Indian nuclear programme.
The method of energy analysis proceeds in two stages. The first stage, called Static Energy Analysis, estimates the energy used in the construction of a single reactor system and also the energy output from the same reactor. The second stage called Dynamic Energy Analysis, compares the energy output of the whole program, as a function of time over a given period, with the energy invested into the programme during the same period.
In this study, the unit of mass is the metric ton. The energy unit used is the kilowatthour and the energy of a million kilowatthours is denoted as MkWh. We use the symbol kWhe to denote a kilowatthour of electrical energy and kWht to denote a kilowatthour of thermal energy.
Energy Investments in the Construction of Nuclear Plants
Static energy analysis consists of estimating independently, from aggregated financial data, energy investments for those items for which construction energy data are not available. This category computes the energy used or invested in the construction of capital plant by separating the plant into four components:
1. The Nuclear Reactor and Steam System
2. Electrical Machinery
3. Building and Services
4. Initial Core Assembly
This has been done by Lovins and Price(1975) for the first three items by knowing the cost per kilowatt of the installed power station components 1-3 and using the energy investment data, per unit cost of all four components. This paper updates this energy investment data by using a factor to take into account additional features added in the plants after the Three Mile Island(TMI) accident in March 1979. This factor is the ratio of post-TMI capital cost per kilowatt of installed capacity($2750/kW according to Electrical World, Sept. 1986,p.20) to pre-TMI cost($1100/kW in 1986 constant US dollars) for a 1000 MW nuclear plant. For item 4, the initial core assembly, the paper does the same for the zircalloy cladding used for natural uranium fuel element housing tubes(fuel rods),after Lovins and Price(1975). For the initial core assembly fuel elements, energy investment figures are available per ton of natural uranium fuel used in the Candu reactors but are dependent on ore concentration.
Lovins and Price(1975) have cited published references giving energy investment figures for two limiting ore concentrations: 0.3 (w/w%) U3O8 and 0.007 (w/w%) U3O8. However, according to Nuclear India (Vol.23/No.1,Special Issue, 1984, p.7): “During the last three decades, various ores totaling 73000 tons of U3O8 in grades ranging from 0.015 w/w% to 0.07 w/w% U3O8 have been identified”. Accordingly, this paper uses the data on energy requirement for the limiting ore concentrations 0.3% and 0.007% to estimate the energy investment to assemble the initial core of uranium oxide elements for the Indian ores of 0.015% and 0.07% concentrations respectively in a Candu reactor of 1000 MW capacity.
The Nuclear Reactor and Steam System
This system, including containment devices, safety and control systems, steam circuits and heat exchangers for a 1000 MW Candu reactor system, has been estimated to have an energy investment of (5025 + 1150) MkWht. This is a post- TMI estimate.
Electrical Machinery
This includes generators, power transformers, control and switchgear and distribution links to grid. These have been estimated to require an investment of (4290+ 825) MkWht, post-TMI.
Buildings and Services
This includes the site, offices, buildings for housing equipment, cooling towers, service requirements and provision of required water supply. The energy investments are estimated to be (2170+350) MkWht.
The Initial Core Assembly
This contains an initial supply of fuel amounting to about one-eighth of the total fuel which the reactor will consume in its twenty-five year lifetime. A nuclear station cannot start functioning at all until the complete core has been assembled. This is an investment because the energy and finances for the construction and assembly of the initial core must be spent before the reactor can produce energy. This would be equivalent to having about 15 million tons of coal in a 1000 MW super thermal fossil- fired power station before start- up. The estimate of energy investment for the zircalloy tubes housing the fuel elements in this assembly amounts to (1560+ 150) MkWht(Lovins and Price 1975). The estimate for the energy investments for the fuel elements is made next.
Uranium Fuel: Estimate of Energy Investment
Energy is consumed in the following processes to extract uranium from its ore in the first place and convert to uranium hexafluoride and thence to uranium-oxide pellets.
Mining and Milling for U3O8 Extraction
According to Lovins and Price(1975), ore of 0.3 w/w% U3O8 consumes 0.265 MkWht energy per ton uranium, while ore of 0.007 w/w% U3O8 consumes (0.74(e)+ 8.22(t)) MkWh per ton of natural uranium. At a conversion efficiency of 25% for thermal to electrical energy, the energy investment for mining and milling 0.007 w/w% U3O8 ore to useful natural uranium is 11.18 MkWht per ton. This is 42.2 times the energy investment for mining and milling 0.3 w/w% U3O8 ore. Now the two concentrations are in the ratio 0.3/0.007=42.857 which is within 1.56% of the energy ratio 42.2 for processing the two ores. The close matching of the energy ratio and the inverse of the concentration ratio is of course to be expected if the same quantity of useful uranium is to be obtained by the mining and milling process. Thus we get the formula
E.C = constant= 0.07826 MkWht per ton,
where E is the energy investment in MkWht per ton of uranium extracted and C is the w/w/% U3O8 concentration in ore. Using this equation, the energy investment for mining and milling of Indian uranium ores of various concentrations can be computed. On this basis, the energy investment for this part of the process for 0.015 w/w% U3O8 ore works out to 5.2173 MkWht per ton uranium, and for 0.07 w/w% U3O8 ore to 1.118 MkWht per ton uranium.
Conversion to Uranium Hexafluoride
The mined and milled product is next converted to uranium hexafluoride. All grades of ore require the same amount of energy for this stage which is given by (0.016(e)+ 0.054(t)) MkWh per ton uranium. Using the factor 4 to convert electrical to thermal units, we get the energy invested for conversion to uranium hexafluoride to be 0.118 MkWht per ton uranium.
Conversion to Uranium dioxide or Similar Solid Fuel Material and Fabrication into Fuel Elements
In this final stage of preparing natural uranium fuel the energy invested is given by (0.048(e) + 0.032(t)) MkWh /ton uranium. Or with conversion factor of 4 for electrical to thermal units, we have the energy invested for conversion to uranium dioxide and fabrication to uranium fuel elements to be 0.224 MkWht/ton uranium.
Energy Invested to make Initial Core Assembly for a 1000 MW Candu Reactor
A 1000 MW Candu reactor requires initial core of 182 tons of natural uranium fuel. The energy investment for this initial core assembly using 0.015 w/w% U3O8 and 0.07 w/w% U3O8 ores respectively, have been worked out and collected in Table 1. From this table we see that a 1000 MW Candu reactor imposes an energy investment for initial core assembly of 1011.8 MkWht for 0.015 w/w% ore and 265.7 MkWht for 0.07 w/w% ore.
Energy Investment for Heavy Water
Lovins and Price(1975) cite figures of the Heavy Water Division of the Atomic Energy of Canada for the estimates for energy required to make a ton of heavy water to be (0.65(e)+ 6(t)) MkWh. The Candu reactor uses heavy water as moderator of 0.3 ton/MW and as a coolant of 0.4 ton/MW. Thus for a 1000 MW Candu reactor the heavy water requirements are 5990 MkWht. To produce a unit of output under Indian conditions it is more energy intensive than in the EEC or Japan or the US. For instance, the cement industry in India is about 24% more energy intensive than in the West(Jagus 1981). Since the data used in our paper are for UK conditions as cited in Lovins and Price(1975), the results obtained may be expected to be only a conservative estimate.
Total Energy Investments for Construction of a 1000 MW Candu Reactor
The total energy investments (post- TMI) have been collected in Table 2 for the separate station components. It may be seen that an investment energy requirement of about 20,000 million kilowatthours goes towards the construction of a 1000 MW Candu reactor.
Computation of Energy Output from a Nuclear Station
Gross and Net Outputs
A nuclear station sends out an amount of electricity per year which is a fraction of the amount which would be sent out annually if the station operated continuously at its full design rating. Also, before the electricity reaches the user some of the elctricity is used up in heating the transmisssion lines and these are termed transmission losses. The average All-India figure seems to be, in this instance, actually, of the order of 22%. Still, let us, for the present, settle for 7.5% losses in transmission and 3.75%(50% of 7.5%) in further activities that support electricity generation. On this basis, we allow for only 11.25% losses. We shall assume a capacity factor of 62%. On this basis a Candu 1000 MW nuclear reactor station delivers energy at the rate of (1000 MW*0.62*0.8875*8760*1000) kWh per year which is 4820.19 MkWh per year. A year is taken as consisting of 8760 hours.
Process Inputs to be Subtracted from the Annual Output
Annual Uranium Re-load Fuel Requirement
Every year a certain portion of the output goes towards the energy invested in preparing nuclear fuel used to refuel the reactor. For a 1000 MW Candu reactor the requirement every year for refuelling is 67 tons of natural uranium. The energy requirement to produce this fuel is given in Table 1. Only because the reactor would now be in operation with its initial fuel, it is assumed that this energy would be directly forthcoming from the reactor itself. Thus this is directly offset from the electrical output per year. For 67 tons of natural uranium the energy investment is 372.5 MkWh from Table 1 for 0.015 w/w% U3O8 ore.
Annual Heavy Water Requirement
Every year about 0.7% of heavy water ina 1000 MW Candu reactor is lost(4.9 tons). The energy required to produce this heavy water is 42 MkWh which is again, for the same reason as above, subtracted from the annual energy output of the reactor.
Net Output of the Nuclear Reactor
When we subtract items calculated above from the annual output of a reactor of 4820 MkWh, we get for 0.015 w/w% ore, the net electrical output of the reactor to be 4405 MkWh. For a 0.07 w/w% U3O8 ore, the output of the reactor on the same lines works out to be 4680 MkWh of electricity.
Static Energy Analysis of a 1000 MW Candu Reactor
The input per year as well as the output per year of a 1000 MW Candu reactor have been worked out in the foregoing sections and are consolidated in Table 3, which shows also the annual energy output to annual energy input ratio. Note that the uncertainties involved in energy input are + 184 MkWh. For a detailed discussion of these see Lovins and Price(1975). Because of these uncertainties, values for input of (2510+184) MkWh are all shown.
Energy Investments Neglected in the Analysis
The following energy investments have not been accounted for in the above analysis.
1. Building electrical transmission and distribution facilities and building special plants like pumped storage hydro schemes that may be required to compensate for the effects of nuclear stations on the security and economics of the grid.
2. Building supporting facilities for the nuclear fuel cycle-a reprocessing plant,fuel conversion and fabrication plant, transport facilities and a heavy water manufacturing plant. In an unfolding nuclear power programme, substantial energy inputs are required to build these ancillaries well in advance of obtaining electrical power inputfrom the programme. Some of the facilities like the Indian heavy water plants, although highly capital intensive as well as energy intensive to construct, have operated at rather low capacity factors. For instance, the Tuticorin heavy water plant has 20% plant factor, making poor use of the energy invested in constructing them.
3. Process inputs are considered on the basis of electricity sent out sent out rather than gross energy generated. Hence energy needed to opearte auxiliaries will be additional.
4. Research and development input-a rather gargantuan investment.
5. Administrative overheads: design, safety analysis and precautions, other regulatory efforts, health physics monitoring, accounting,paper consumed and so on.
6. Alternative land use including all other natural inputs like sunshine, rain, wind, soil fertility of all nuclear facilities.
7.Energy requirements of accidents, requirements for decontamination, evacuation, new construction, and abandonment of land. In Chernobyl, an estimate of energy requirement was upwards of 44000 MkWh. But the abandoned land -a radius of 30 km or more than 2779 km^2 represents an energy input loss of 6,00,000 MW or more based on solar energy input of 240 watts per square meter. With 750,000 people dying from cancer according to one probability estimate, the energy requirements are difficult to quantify except putting it at an inestimably high value(Flavin 1987,Mebb 1986).
8. Energy inputs associated with decommissioning defunct reactors like in Rajasthan for the RAPP unit: One estimate puts the energy requirement at more than the entire life production of the reactor(Lovins and Price, 1975).
9. Energy inputs associated with transport,treatment, storage, and disposal of low and medium level radioactive wastes.
10. The disposal and storage of high level wastes: all process and investment requirement for transporting, treating, sorting, retrieving, safeguarding and disposal of high level wastes.
Energy Invested in Waste Storage
The disposal technologies are speculative. So is the appropriateness of storage options proposed. In the absence of credible disposal methods, the use of steel canisters for successive 100 year proposed surface storage methods will be examined for energy intensity. These refer to high level radioactive wastes. Over very long periods, these energy inputs would equal or exceed, by orders of magnitude, the life time gross outputs of the reactors served.
The average of all the ratios given in Table 3 is 1.85. Let us however consider, as an illustration, the case of 0.015 w/w% U3O8 ore. Corresponding to this, the annual energy output from a 1000 MW Candu reactor would be 4405 MkWh.(Table 3). Considering an energy output /input ratio of 1.75, the energy input per year is 2510 MkWh. If we consider a steel canister cited in Lovins and Price(1975)(pp 96-97) for a surface storage tank it consumes 100 kW every year for its maintenance. Thus annually, the energy used for storage of high level wastes from the reactor works out to 0.876 MkWh. Let us consider an annual energy output / annual energy input ratio of less than 1.75, say 1.39, and see how many years of surface storage such a reactor can provide energy for during its lifetime.Note that the ratio 1.39 corresponds to a plant factor of 50% without debiting any energy consumed for surface storage maintenance. Multiplying the annual energy input of 2510 MkWh by 1.39 we get the energy output of the reactor working at 62% plant factor per year after debiting energy for surface storage to be 3489 MkWh per year. Since the output per year before this debit is 4405 MkWh per year, the energy debited to waste storage maintenance works out to (4405-3489)=916 MkWh per year. Over the 25 year lifetime of the reactor, the energy available for supply to the steel tank is 916*25 or 22902 MkWh. The energy consumed by the canister being 0.876 MkWh per year, the number of years of waste storage served by this reactor is 22902/0.876 = 26144 years.
This is only slightly more than he half life of the dominant isotope of high level wastes such as Plutonium 239, which is 24390 years. Clearly we require at least 500,000 years of storage for this which is about 20 times that made available in the above manner. But this corresponds to about 4 times the energy delivered by the reactor during its entire lifetime. Thus the ratio 1.39 considering a bit of ‘future services’ is just not enough. According to Issacson and Brownell(1973) the required periods of isolation for actinides like Plutonium 239 and Neptunium 237 are a million years and a hundred million years respectively! Thus we have to go deep down until there is absolutely no net energy even from a single reactor. Less energy intensive methods are at present not available. Hence in the absence of viable methods already demonstrated and ready for assessment , the existing methods of storage may have to be used for all time.
Lovins and Price(1975) state that ‘it is precisely this very possibility that has led the United States Environmental Protection Agency to reject(proposed surface storage methods) as inadequate’. The solution to the high level waste problem is ‘transcientific’. The critical problem of disposal is that the degree of permanence needed subjects any scheme to geological requirements and the enormous time-span involved reduces the relevance of any empirical data to a low value. There is thus no scientific evidence that vitrified solidified high level wastes in deep geological formations forming a central repository will remain in one piece, be insoluble, or inert over periods considerably shorter than these. Further no responsible geologist can offer a guarantee. The disposal should and must be retrievable, which then also means surveillance over geological time scales far exceeding the period of human experience of observed cultures(Tolstoy 1986,Boyle 1986, Lovins and Price1975).
An idea of the mess the nuclear enterprise has landed itself in can be gleaned from the fact that in the US, the Department of Energy is committed to spending 2.5 billion dollars(about 4000 Cr 1989 Rupees) over the next five year period till 1992 to solve the high level waste disposal problem. A number of states in the US have enacted legislation denying electric utilities the option to build new nuclear power plants until proven disposal techniques are developed(Electrical World, July 1986).
Performance of Indian Nuclear Stations
According to an advertisement supplement in the Times of India dated October 16th 1987, taken out by the Nuclear Power Corporation, the average yearly capacity factor of all the nuclear power plants from 1969 to July 1987(about 18 years) works out to 46.26%. Compare this with the boiling water GE reactor in US(58% for 1968-84 and 51.2% in 83-84) and for Canada:Average lifetime capacity factor 77.1%. The Indian Nuclear performance in the three recent years has been, on the aggregate, 46.27& for 1985-86,46.62 in 1986-87, and 46.67 in 1987-88. Thus if the Indian Nuclear Power Programme, from now on, maintains an average plant (or capacity) factor of 62%, the overall plant factor between 1969 to 2001 AD would be about 53.4%. But the assumption of a jump from a historical 46.47% to 62% on a sustained basis for the plant factor may not be warranted for the same reasons that are ascribed to the programme’s past performance, with some additional ones thrown in, like untried 500 MW designs and probably lack of sufficient heavy water in time, unfamiliar new types of reactors, and, of course, accidents. Thus we may consider a plant factor of 50%an average plant factor till 2001 from now, for purposes of our analysis and see the implications.
Output/Input Ratio for a Plant factor of 50%
With a construction energy input per year for a 1000 MW Candu reactor of 2510 MkWh and an energy output per year corresponding to 50% plant factor and about 11% transmission losses of 3484 MkWh the output per year to input per year ratio would be 1.39. We note that this ratio does not make any allowance for energy required for storage of high level wastes. Thus the output/input ratio for the Indian Nuclear Power programme could easily be less than that indicated for by this analysis. Om account of economies of scale, as far as the construction energy is concerned, units of less than 1000 MW size would have a lower output/input ratio than a 1000 MW reactor. For computing the energy balance of the Indian programme to 2001 AD we shall take a ratio of 1.39 and compare it with other ratios for implications.
Energy Balance for the Indian Nuclear Programme 1985-2001 AD
This energy balance will be carried out on the basis of the capacity build- up data furnished in the supplement issued by the NPC in the newspapers on October 16th, 1987.
As per data published in an NPC supplement in the Times of India dated October 16th 1987, the capacity build-up is as indicated in Table 4. The energy delivered at 62% plant factor and at 50% plant factor is also shown in the Table. It is seen from Table 4 that the energy delivered during the period 1985-2001 AD would for 0.015 w/w% U3O8 ore total 200626 MkWh and for 0.07 w/w% U3O8 ore 216444 MkWh, both at 50% plant factor. In both cases transmission losses are assumed to be 11%. As against this, the energy invested in the construction of theses plants would be (201774+14824) MkWh for 0.015 w/w% U3O8 ore and (194277+14824) MkWh for 0.07 w/w% U3O8 ore. The energy delivered by by these plants at 50% plant factor during 1985-2001 AD would at most therefore equal the heat energy utilised in the construction of these reactors. We should also debit some energy towards maintenance of storage tanks for high level radioactive wastes , against energy delivered during these 17 years. Further we have not considered the construction energy of those reactors which will become operational after 2001 AD, but which willhave to be taken in hand during the period till 2001 AD.
Thus we see that during this period we get no energy at all on balance from these reactors. Just imagine that society would be paying for this electricity, delivered at 85 paise per kWh(1988 prices), some 17900 crores of rupees, or, since the cost of electricity has now become of the order of Re.1/- per kWh, Rs. 21000 Cr(1989 prices) and society will, on balance, have received nothing because the heat energy of high quality withdrawn from society during this period equals the electricity delivered. The net cost to society is therefore infinite per unit energy received during this transaction.
Today the requirements for construction energy for these reactors are met aminly by fossil fuels in India. The major portion of high quality energy required for the construction of nuclear plants is consumed as heat in steel and cement. An idea of the cost of this heat energy can be obtained by a comparison of heat and electricity inputs in the industrial sector in terms of quantity and cost in India. This is brought out in Table 6. Using a conversion factor of 4 for electrical to thermal kilowatthours, the total energy input in the industrial sector per annum from table 6 evaluates to 652865 MkWh(t). The electricity consumption per year 60,000 MkWh(e). Thus the electricity consumption forms 9.19% of the total energy input. The total cost of the other energy inputs-coal and petroleum inputs amounts amounts to 4700 crores of rupees. The corresponding energy consumed being 412865 MkWh. Thus the average cost of coal and petroleum fuel inputs is 11.38 paise per kWh.
Now the cost of electricity from 2*235 MW nuclear reactors according to NPC would be 85 paise per kWh for units commissioned in 1992. This assumes a capital cost of 15405 rupees per kilowatt of installed capacity. But post TMI and post Chernobyl costs would be nearer 2.5 times this amount if the requisite improvements are incorporated which means a cost per unit of electricity delivered of 0.85*2.5=Rs.2.1. If we assume a rise in heat energy cost to, say, 21 paise per kWh, we can expect electricity from a nuclear plant to cost ten times the heat energy cost.
In Table 7, the share of heat and electricity consumptions in the industrial sector is given. The potential for energy conservation in all these is of the order of 20 to 30% only(National Productivity Council, Report on Utilisation and Conservation of Energy, New Delhi, 1983). Thus the nuclear enterprise would consume in these 17 years 1985-2001 AD, high quality cheap heat energy of premium fuels by withdrawing these from society and deliver, during the same period, ten times costlier electricity equal to about the quantum of heat taken away. But as brought out in Table 7 less than 10% of energy requirements of the entire society is in electrical form. What is needed to an extent of 95% at any given period and which was available for say 20 paise per kWh is replaced by something the requirement for which is hardly 5 to 10% and at ten times the cost(Really at infinite real cost according to our finding above!).
Thus the consumer may be led to change over from his simple equipment to devices using electricity alone which would be costlier both as regards equipment as well as electricity charges. And this is done by the nuclear industry by converting nuclear fuels at 28% thermal efficiency. Thus during the 1985-2001 AD period, in the nuclear industry, fuel stocks consumed are 3.57 units nuclear fuel plus one unit fossil fuel in the construction of nuclear facilities, to give back net one unit of electricity, out of which only 0.05 units are required by society. Thus the overall “efficiency” of energy delivered to society is 0.05/(3.57+1.0)=0.0109 or 1.09%. This is for the period 1985-2001 or some three five year plan periods or more.
What are the consequences of such a needless conversion? Neither Table 5 nor Table 7 shows such a massive need for electricity. The result is entirely predictable. State electricity boards like in Sweden and France having created vast surpluses of electricity from fuel, which could have been directly and enormously(in fact infinitely) more efficiently used for producing heat, now subsidise the use of electricity for heating at low temperatures! Thus the path followed is from generation of high quality heat from fossil fuels to build nuclear plants, which output less electricity than the energy used in their construction because of the enormous requirement of energy needed to maintain waste storage devices for infinitely(more than hundred million years) long periods to subsidise immediate use of infinitely costly nuclear electricity to produce low quality heat!
France thus sells its electricity across the channel to surplus electricity Britain which is busy creating more surplus electricity by building nuclear plants which the public do not want! And when there is glut... Look at this report from France(Modern Power Systems, August 1987): EdF has a virtual moratorium on reactor orders and the slow down in orders from EdF has forced Framatome,a nuclear reactor manufacturer, to close down one plant. EdF is the French State electricity board. But in the US market forces and public opinion have found other arrangements for meeting the demand for energy. And Sweden is phasing out its 9435 MW of nuclear electricity capacity by 2010. But in India we are supposed to look forward to the Fast Breeders as a lasting source like France. The potential, for extreme danger, of such lasting sources of untested-for-feasibility reactors, has been vividly brought out by R. E . Webb who made a detailed study of the West German SNR 300 reactor of the fast breeder type and found that it can explode like several Hiroshimas(Webb 1986).
Forests are the perfect way to convert nuclear energy to use, nuclear energy of the most advanced form, viz. fusion in the sun located safely, ecologically appropriately, some 150 million kilometers away from the earth.
References
1. Flavin C.1987. Reassessing Nuclear Power:The Fallout from Chernobyl.pp 18-19. Paper No.75.Worldwatch Institute..Washington D.C., March.
2. Ghosh S.1984. “Development: The Real options”. The Ill. Wkly.Ind. June 24-30, p 43.
3. Issacson R.E and Brownell L.E.1973.”Ultimate Storage of Radioactive Wastes in Terrestrial Environments”. In OECD-NEA/IAEA. Management of Radioactive Wastes from Fuel Reprocessing. OECD 66 73 02 3. p.955. Quoted in Lovins et al (op cit) p.34 and p.85-86.
4. Jagus P.J.1981.Energy Profile of the Indian Cement Industry. In “Workshop on Energy: Paper and Cement Industries”. The Industrial and Credit and Investment Corporation of India Limited, Bombay. Summary Proc. And Papers. p.303.
5. Lovins A.B and Price J.H.1975. Non-nuclear Futures: The Case for an Ethical Energy Strategy. Harper-Colophon Books. Harper & Row, Publishers. Sao Paulo.pp.181-190;pp96-97.
6. Tolstoy.I.1986. “High Level Waste: No Technical Solution”. The Ecologist.Vol.16,No.4/5,pp.205-209. Also Boyle S.(in the same issue).”Nuclear Waste-The Unsolved Problem”.
7. Webb R.E.1986. “Western Reactors: How They Compare With Chernobyl ”. The Ecologist. op cit. Pp.166-167. Also,”The Health Consequences of Chernobyl”. The Ecologist. Op cit. pp.169-170, and The Ecologist. No.6.1986..Vol.16.
TABLES








By R. Ashok Kumar,B.E.,M.E., Negentropist, Bombay Sarvodaya Mandal, 299,Tardeo Road, Nana Chowk, Mumbai-400007.
E-mail: rakumra@yahoo.com
29 November 2004
© 2017 Ramaswami Ashok Kumar
http://enenews.com/nuclear-expert-it-is-not-advisable-to-eat-bluefin-tuna-radiation-deposited-over-600000-sq-miles-of-pacific-cesium-crosses-placental-barrier-of-animals
When the energy audit is negative, the risks are adversely high leading to extinction level events.
It is absolutely essential to reexamine the Indian Nuclear Energy Programme in the light of its adverse energy audit. Here an audit of 1000 MW nuclear power plants is performed with the plan of having 24000 MW stabilised on line by 2025 AD. It is envisaged by Dr MR Srinivasan, former AEC Chair, who wrote recently in the Hindu on the Indian Nuclear Power Scenario, that some 200,000 MW Capacity of an assortment of nuclear plants shall be on line by 2050 AD.
The analysis shows that even a quarter of a century later, by 2025 AD, no nuclear power will be available to society. In fact the Nuclear programme will be still paying back the energy consumed by the nuclear industry, by the time one set of 2 x 1000 MW nuclear reactors are decommissioned in 2025! See Table 1 and Figures 1 and 2 below: One would have thought that as fresh nuclear capacity is added, it would meet the shortage of power demand. In reality, it is never so(Figure 1).Of course, if the government is serious about the decommissioning, it must have energy for this as well, for a century or more. Also, waste management has become lethally serious: In a nation which is aware of the implications, it is worthwhile to note that even after more than half a century, the USA had to find itself in the unenviable position of having to take care of wastes at Yucca mountain site by designing the repository, not for 10,000 years as the Environmental Protection Agency, USA, wanted, but for 300,000 years or more before groundwater radiation exceeded drinking water limits at the boundary of the site as required by scientists at the National academy of Sciences: That practically means : one should be transscientific! Or abandon nuclear power, and the existing sites for storage beside nuke power stations should continue. See court ruling of July 9,2004 at the URL:
http://pacer.cadc.uscourts.gov/docs/common/opinions/200407/01-1258a.pdf
This article also contains an electronic reproduction of a net energy analysis of the Indian Nuclear Programme as it was envisaged for 1985-2001. This appeared in the PPST Bulletin, No.18,March 1989,pp 10-25. This includes details of construction energy inputs and waste storage inputs used for the analysis. This gives an idea of the output/input ratios of Pressurised Heavy Water Reactors used in India.. In this article waste storage energy debits are included in the dynamic energy analysis. This is because of the extremely slowly deployable nature of the nuclear programme as shown above. This makes the time constant of transients(growth) the same order as the lifetime of the programmes, of interim above ground waste storages, and as the reactors are decommissioned, the need for the programme growth at some constant rate to prolong, albeit, absolutely serving no net energy production purpose except to conspiciously consume finances, energy and power with disastrous consequences to life.
As pointed out before, the Japanese Nuclear Energy Programme and the French are equally adverse regarding the energy audit, as negative as the USA’s.
References:
On Energy Audit of Nuclear Fuel Cycles:
energy audit of nuclear fuel cycles
at http://energyauditofnuclearfuelcycles.blogspot.in/
On health effects of n-power:
http://isisunveiledhenp.blogspot.com/2010/07/health-effects-of-nuclear-power-during.html
http://plutoniumaradiumabillionpeoplehitdna.blogspot.com/
On dual use of n-power byproducts:
http://frozenevolutionofmind.blogspot.com/
or
http://isisunveiled.rediffblogs.com
On the cumulative and synergistic effects of modern civilisation:
Nuclear Fundamentalism
http://nuclearfunda.blogspot.com/
INDIAN NUCLEAR ENERGY PROGRAMME: AN ENERGY AUDIT: NUCLEAR INDUSTRY DEMAND AND CAPACITY BUILD UP:1998-2025(Table 1: Please right click on the blackness and put on separate tab, right click on the black image in the separate tab, then click on image info to view the table!)
Note: In Table 1, please read for energy invested in the nuclear programme, energy invested in the nuclear programme per year.


Figure 1:(Click on the figure to view) Nuclear Capacity Build Up requires that Nuclear Industry Demand be met by thermal power, exacerbating the greenhouse effect substantially, in perpetuity. This is so, even after 2025 as the adverse energy audit goes on and on as the Nuclear Growth continues, in fact many decades more than the life- time of a nuclear reactor.
INDIAN NUCLEAR ENERGY PROGRAMME: AN ENERGY AUDIT(Click to view Figure 2)

Figure 2: The Indian Nuclear Energy Programme is an enormous consumer of high quality energy. As shown, there is no net energy output available to society even 28 years into the programme,assumed to have commenced from 1998. Since the aim is to go ahead with nuclear power even after 2025 when 200000 MW are proposed to be put on line by 2050, the programme will be a perpetual consumer of energy from society, rather than giving any net output.
The paper The Indian Nuclear Energy Programme- A Net Energy Analysis originally published in the PPST Bulletin referred to in the above article follows.
PPST Bulletin, No. 18, March 1989.
The Indian Nuclear Energy Programme- A Net Energy Analysis
By R. Ashok Kumar, B.E.,M.E(Power),Negentropist, Bombay Sarvodaya Mandal, 299, Tardeo Road, Nana Chowk, Mumbai-400007.
E-mail: rakumra@yahoo.com
The article performs an energy audit of the Indian Nuclear Energy Programme over the period 1985-2001. It demonstrates that the annual ratio of output/input over this period is low, thus adversely affecting the net energy output of the programme. This programme is critically dependent on untested methods of disposal of hazardous wastes. Such methods demand a high-volume investment in energy, lasting over several decades, to keep them isolated, which further reduces the efficacy of the nuclear programme.
One of the key conclusions of this study is that the Nuclear Energy Programme consumes so to speak, five times the energy that it is projected to deliver. Such a conclusion is particularly applicable for 1000 MW plant-sizes. The ultimate production pf nuclear energy/electricity comes after 15 years, but, in order to construct, maintain the plants and stabilise the waste disposal system, five times that much energy, in the form of precious fossil fuels are used up, contributing to the melting of the glaciers. Thus it is energetically unfavourable. Worse still, it is unfavourable in monetary terms too, for the electricity produced will be ten times costlier. This after investing an extraordinary volume of energy and money to the tune of Rs. 20,000 Cr(1985 Rupees)(for 10050 MW installed capacity).
It thus seems the Nuclear Energy Programme is designed to fritter away scarce energy resources and capital that will pay less and cost more. Coupled with this is the additional fact that the waste disposal systems involved are untested and even speculative. A plea is made herein to halt immediately the effort wasted on an immature energy conversion technology aas the Nuclear Energy Programme in India.
Introduction
In any large scale programme of installation of thousands of crore of rupees worth of electricity-generating stations, year after year, it is very essential that we first examine
-whether the programme supplies more, in fact much more energy than it consumes in its construction, operation and maintenance;
-how complete the technology is; that is, whether its by-products can be used or absorbed by nature in such a way that nothing is ever wasted;
-to what extent it affects the health of the environment, including all life.
When such a series of exercises were carried out in various parts of the world, it was noticed that nuclear fission technology is immature and not ready for deployment where life exists. We have so evolved that the ecological base assures health, provided we harmonise our behaviour with the rest of all that is. That is why nuclear energy is actively driving the life patterns on this globeby optimally situating itself in the sun 150 million kilometers away. Careful analysis shows that the problem of safety of artificial nuclear power is insoluble. In fact energy audit studies show that without an economical and safe method of disposal of wastes generated by fission technology, the nuclear programme would always be a net consumer of energy. And it was also found, after the most careful of deliberations, that there is no solution at all to the waste disposal problem. Radioactivity should not be created by man in the first place.
Thus, many states in the U.S.A have prohibited the exercise of the nuclear energy option by legislation, unless satisfactorily demonstrated methods of waste disposal are economically and safely possible for all times. Also the market forces inthe US seem to work against adoption of nuclear power. But, most important, the public are becoming extremely vigilant. Still there is the other side and America possesses 75000 MW of the most dangerous nuclear reactors in operation and the commitment is for a total upwards of 100,000 MW. However many of these have been shutdown indefinitely, although the number of those shutdown is not exactly known. Sweden with 9400 MW of nuclear power, has adopted a policy of phasing out nuclear power by 2010 AD. Austria and Philippines have renounced the nuclear option. In Soviet Russia the citizens have protested against the setting up of a nuclear plant at Krasnodar. In Kaiga, in India, people are up against changing their life styles by buying the dangers of nuclear power. The people of Kerala successfully refused a nuclear plant at Peringome.
Since a clear cut energy audit is not readily available for the Indian Nuclear Programme, this article examines the Indian programme by carrying out an energy audit for the period 1985-2001 AD, with the help of available Indian and foreign data. On account of the nature of the problem, safety aspects cannot but be taken into account in the analysis. The capital, construction, operation, maintenance and waste management costs of nuclear plants have escalated considerably since the Three Mile Island and Chernobyl disasters. In view of this, there is an urgent need for a thorough reassessment of the entire nuclear power generation programme. This article purports to highlight the energy aspects of the programme so that an informed debate can be initiated.
The Indian Nuclear Power Programme envisages the construction of Candu type nuclear reactors; the plan is to have a total installed capacity of 10,050 MW by 2001 AD. Candu reactors are the Canadian deuterium-uranium type reactors- heavy water- moderated heavy water-cooled and natural uranium fuelled . We extend the methodology of Lovins and Price(1975) so as to be applicable to the Indian nuclear programme.
The method of energy analysis proceeds in two stages. The first stage, called Static Energy Analysis, estimates the energy used in the construction of a single reactor system and also the energy output from the same reactor. The second stage called Dynamic Energy Analysis, compares the energy output of the whole program, as a function of time over a given period, with the energy invested into the programme during the same period.
In this study, the unit of mass is the metric ton. The energy unit used is the kilowatthour and the energy of a million kilowatthours is denoted as MkWh. We use the symbol kWhe to denote a kilowatthour of electrical energy and kWht to denote a kilowatthour of thermal energy.
Energy Investments in the Construction of Nuclear Plants
Static energy analysis consists of estimating independently, from aggregated financial data, energy investments for those items for which construction energy data are not available. This category computes the energy used or invested in the construction of capital plant by separating the plant into four components:
1. The Nuclear Reactor and Steam System
2. Electrical Machinery
3. Building and Services
4. Initial Core Assembly
This has been done by Lovins and Price(1975) for the first three items by knowing the cost per kilowatt of the installed power station components 1-3 and using the energy investment data, per unit cost of all four components. This paper updates this energy investment data by using a factor to take into account additional features added in the plants after the Three Mile Island(TMI) accident in March 1979. This factor is the ratio of post-TMI capital cost per kilowatt of installed capacity($2750/kW according to Electrical World, Sept. 1986,p.20) to pre-TMI cost($1100/kW in 1986 constant US dollars) for a 1000 MW nuclear plant. For item 4, the initial core assembly, the paper does the same for the zircalloy cladding used for natural uranium fuel element housing tubes(fuel rods),after Lovins and Price(1975). For the initial core assembly fuel elements, energy investment figures are available per ton of natural uranium fuel used in the Candu reactors but are dependent on ore concentration.
Lovins and Price(1975) have cited published references giving energy investment figures for two limiting ore concentrations: 0.3 (w/w%) U3O8 and 0.007 (w/w%) U3O8. However, according to Nuclear India (Vol.23/No.1,Special Issue, 1984, p.7): “During the last three decades, various ores totaling 73000 tons of U3O8 in grades ranging from 0.015 w/w% to 0.07 w/w% U3O8 have been identified”. Accordingly, this paper uses the data on energy requirement for the limiting ore concentrations 0.3% and 0.007% to estimate the energy investment to assemble the initial core of uranium oxide elements for the Indian ores of 0.015% and 0.07% concentrations respectively in a Candu reactor of 1000 MW capacity.
The Nuclear Reactor and Steam System
This system, including containment devices, safety and control systems, steam circuits and heat exchangers for a 1000 MW Candu reactor system, has been estimated to have an energy investment of (5025 + 1150) MkWht. This is a post- TMI estimate.
Electrical Machinery
This includes generators, power transformers, control and switchgear and distribution links to grid. These have been estimated to require an investment of (4290+ 825) MkWht, post-TMI.
Buildings and Services
This includes the site, offices, buildings for housing equipment, cooling towers, service requirements and provision of required water supply. The energy investments are estimated to be (2170+350) MkWht.
The Initial Core Assembly
This contains an initial supply of fuel amounting to about one-eighth of the total fuel which the reactor will consume in its twenty-five year lifetime. A nuclear station cannot start functioning at all until the complete core has been assembled. This is an investment because the energy and finances for the construction and assembly of the initial core must be spent before the reactor can produce energy. This would be equivalent to having about 15 million tons of coal in a 1000 MW super thermal fossil- fired power station before start- up. The estimate of energy investment for the zircalloy tubes housing the fuel elements in this assembly amounts to (1560+ 150) MkWht(Lovins and Price 1975). The estimate for the energy investments for the fuel elements is made next.
Uranium Fuel: Estimate of Energy Investment
Energy is consumed in the following processes to extract uranium from its ore in the first place and convert to uranium hexafluoride and thence to uranium-oxide pellets.
Mining and Milling for U3O8 Extraction
According to Lovins and Price(1975), ore of 0.3 w/w% U3O8 consumes 0.265 MkWht energy per ton uranium, while ore of 0.007 w/w% U3O8 consumes (0.74(e)+ 8.22(t)) MkWh per ton of natural uranium. At a conversion efficiency of 25% for thermal to electrical energy, the energy investment for mining and milling 0.007 w/w% U3O8 ore to useful natural uranium is 11.18 MkWht per ton. This is 42.2 times the energy investment for mining and milling 0.3 w/w% U3O8 ore. Now the two concentrations are in the ratio 0.3/0.007=42.857 which is within 1.56% of the energy ratio 42.2 for processing the two ores. The close matching of the energy ratio and the inverse of the concentration ratio is of course to be expected if the same quantity of useful uranium is to be obtained by the mining and milling process. Thus we get the formula
E.C = constant= 0.07826 MkWht per ton,
where E is the energy investment in MkWht per ton of uranium extracted and C is the w/w/% U3O8 concentration in ore. Using this equation, the energy investment for mining and milling of Indian uranium ores of various concentrations can be computed. On this basis, the energy investment for this part of the process for 0.015 w/w% U3O8 ore works out to 5.2173 MkWht per ton uranium, and for 0.07 w/w% U3O8 ore to 1.118 MkWht per ton uranium.
Conversion to Uranium Hexafluoride
The mined and milled product is next converted to uranium hexafluoride. All grades of ore require the same amount of energy for this stage which is given by (0.016(e)+ 0.054(t)) MkWh per ton uranium. Using the factor 4 to convert electrical to thermal units, we get the energy invested for conversion to uranium hexafluoride to be 0.118 MkWht per ton uranium.
Conversion to Uranium dioxide or Similar Solid Fuel Material and Fabrication into Fuel Elements
In this final stage of preparing natural uranium fuel the energy invested is given by (0.048(e) + 0.032(t)) MkWh /ton uranium. Or with conversion factor of 4 for electrical to thermal units, we have the energy invested for conversion to uranium dioxide and fabrication to uranium fuel elements to be 0.224 MkWht/ton uranium.
Energy Invested to make Initial Core Assembly for a 1000 MW Candu Reactor
A 1000 MW Candu reactor requires initial core of 182 tons of natural uranium fuel. The energy investment for this initial core assembly using 0.015 w/w% U3O8 and 0.07 w/w% U3O8 ores respectively, have been worked out and collected in Table 1. From this table we see that a 1000 MW Candu reactor imposes an energy investment for initial core assembly of 1011.8 MkWht for 0.015 w/w% ore and 265.7 MkWht for 0.07 w/w% ore.
Energy Investment for Heavy Water
Lovins and Price(1975) cite figures of the Heavy Water Division of the Atomic Energy of Canada for the estimates for energy required to make a ton of heavy water to be (0.65(e)+ 6(t)) MkWh. The Candu reactor uses heavy water as moderator of 0.3 ton/MW and as a coolant of 0.4 ton/MW. Thus for a 1000 MW Candu reactor the heavy water requirements are 5990 MkWht. To produce a unit of output under Indian conditions it is more energy intensive than in the EEC or Japan or the US. For instance, the cement industry in India is about 24% more energy intensive than in the West(Jagus 1981). Since the data used in our paper are for UK conditions as cited in Lovins and Price(1975), the results obtained may be expected to be only a conservative estimate.
Total Energy Investments for Construction of a 1000 MW Candu Reactor
The total energy investments (post- TMI) have been collected in Table 2 for the separate station components. It may be seen that an investment energy requirement of about 20,000 million kilowatthours goes towards the construction of a 1000 MW Candu reactor.
Computation of Energy Output from a Nuclear Station
Gross and Net Outputs
A nuclear station sends out an amount of electricity per year which is a fraction of the amount which would be sent out annually if the station operated continuously at its full design rating. Also, before the electricity reaches the user some of the elctricity is used up in heating the transmisssion lines and these are termed transmission losses. The average All-India figure seems to be, in this instance, actually, of the order of 22%. Still, let us, for the present, settle for 7.5% losses in transmission and 3.75%(50% of 7.5%) in further activities that support electricity generation. On this basis, we allow for only 11.25% losses. We shall assume a capacity factor of 62%. On this basis a Candu 1000 MW nuclear reactor station delivers energy at the rate of (1000 MW*0.62*0.8875*8760*1000) kWh per year which is 4820.19 MkWh per year. A year is taken as consisting of 8760 hours.
Process Inputs to be Subtracted from the Annual Output
Annual Uranium Re-load Fuel Requirement
Every year a certain portion of the output goes towards the energy invested in preparing nuclear fuel used to refuel the reactor. For a 1000 MW Candu reactor the requirement every year for refuelling is 67 tons of natural uranium. The energy requirement to produce this fuel is given in Table 1. Only because the reactor would now be in operation with its initial fuel, it is assumed that this energy would be directly forthcoming from the reactor itself. Thus this is directly offset from the electrical output per year. For 67 tons of natural uranium the energy investment is 372.5 MkWh from Table 1 for 0.015 w/w% U3O8 ore.
Annual Heavy Water Requirement
Every year about 0.7% of heavy water ina 1000 MW Candu reactor is lost(4.9 tons). The energy required to produce this heavy water is 42 MkWh which is again, for the same reason as above, subtracted from the annual energy output of the reactor.
Net Output of the Nuclear Reactor
When we subtract items calculated above from the annual output of a reactor of 4820 MkWh, we get for 0.015 w/w% ore, the net electrical output of the reactor to be 4405 MkWh. For a 0.07 w/w% U3O8 ore, the output of the reactor on the same lines works out to be 4680 MkWh of electricity.
Static Energy Analysis of a 1000 MW Candu Reactor
The input per year as well as the output per year of a 1000 MW Candu reactor have been worked out in the foregoing sections and are consolidated in Table 3, which shows also the annual energy output to annual energy input ratio. Note that the uncertainties involved in energy input are + 184 MkWh. For a detailed discussion of these see Lovins and Price(1975). Because of these uncertainties, values for input of (2510+184) MkWh are all shown.
Energy Investments Neglected in the Analysis
The following energy investments have not been accounted for in the above analysis.
1. Building electrical transmission and distribution facilities and building special plants like pumped storage hydro schemes that may be required to compensate for the effects of nuclear stations on the security and economics of the grid.
2. Building supporting facilities for the nuclear fuel cycle-a reprocessing plant,fuel conversion and fabrication plant, transport facilities and a heavy water manufacturing plant. In an unfolding nuclear power programme, substantial energy inputs are required to build these ancillaries well in advance of obtaining electrical power inputfrom the programme. Some of the facilities like the Indian heavy water plants, although highly capital intensive as well as energy intensive to construct, have operated at rather low capacity factors. For instance, the Tuticorin heavy water plant has 20% plant factor, making poor use of the energy invested in constructing them.
3. Process inputs are considered on the basis of electricity sent out sent out rather than gross energy generated. Hence energy needed to opearte auxiliaries will be additional.
4. Research and development input-a rather gargantuan investment.
5. Administrative overheads: design, safety analysis and precautions, other regulatory efforts, health physics monitoring, accounting,paper consumed and so on.
6. Alternative land use including all other natural inputs like sunshine, rain, wind, soil fertility of all nuclear facilities.
7.Energy requirements of accidents, requirements for decontamination, evacuation, new construction, and abandonment of land. In Chernobyl, an estimate of energy requirement was upwards of 44000 MkWh. But the abandoned land -a radius of 30 km or more than 2779 km^2 represents an energy input loss of 6,00,000 MW or more based on solar energy input of 240 watts per square meter. With 750,000 people dying from cancer according to one probability estimate, the energy requirements are difficult to quantify except putting it at an inestimably high value(Flavin 1987,Mebb 1986).
8. Energy inputs associated with decommissioning defunct reactors like in Rajasthan for the RAPP unit: One estimate puts the energy requirement at more than the entire life production of the reactor(Lovins and Price, 1975).
9. Energy inputs associated with transport,treatment, storage, and disposal of low and medium level radioactive wastes.
10. The disposal and storage of high level wastes: all process and investment requirement for transporting, treating, sorting, retrieving, safeguarding and disposal of high level wastes.
Energy Invested in Waste Storage
The disposal technologies are speculative. So is the appropriateness of storage options proposed. In the absence of credible disposal methods, the use of steel canisters for successive 100 year proposed surface storage methods will be examined for energy intensity. These refer to high level radioactive wastes. Over very long periods, these energy inputs would equal or exceed, by orders of magnitude, the life time gross outputs of the reactors served.
The average of all the ratios given in Table 3 is 1.85. Let us however consider, as an illustration, the case of 0.015 w/w% U3O8 ore. Corresponding to this, the annual energy output from a 1000 MW Candu reactor would be 4405 MkWh.(Table 3). Considering an energy output /input ratio of 1.75, the energy input per year is 2510 MkWh. If we consider a steel canister cited in Lovins and Price(1975)(pp 96-97) for a surface storage tank it consumes 100 kW every year for its maintenance. Thus annually, the energy used for storage of high level wastes from the reactor works out to 0.876 MkWh. Let us consider an annual energy output / annual energy input ratio of less than 1.75, say 1.39, and see how many years of surface storage such a reactor can provide energy for during its lifetime.Note that the ratio 1.39 corresponds to a plant factor of 50% without debiting any energy consumed for surface storage maintenance. Multiplying the annual energy input of 2510 MkWh by 1.39 we get the energy output of the reactor working at 62% plant factor per year after debiting energy for surface storage to be 3489 MkWh per year. Since the output per year before this debit is 4405 MkWh per year, the energy debited to waste storage maintenance works out to (4405-3489)=916 MkWh per year. Over the 25 year lifetime of the reactor, the energy available for supply to the steel tank is 916*25 or 22902 MkWh. The energy consumed by the canister being 0.876 MkWh per year, the number of years of waste storage served by this reactor is 22902/0.876 = 26144 years.
This is only slightly more than he half life of the dominant isotope of high level wastes such as Plutonium 239, which is 24390 years. Clearly we require at least 500,000 years of storage for this which is about 20 times that made available in the above manner. But this corresponds to about 4 times the energy delivered by the reactor during its entire lifetime. Thus the ratio 1.39 considering a bit of ‘future services’ is just not enough. According to Issacson and Brownell(1973) the required periods of isolation for actinides like Plutonium 239 and Neptunium 237 are a million years and a hundred million years respectively! Thus we have to go deep down until there is absolutely no net energy even from a single reactor. Less energy intensive methods are at present not available. Hence in the absence of viable methods already demonstrated and ready for assessment , the existing methods of storage may have to be used for all time.
Lovins and Price(1975) state that ‘it is precisely this very possibility that has led the United States Environmental Protection Agency to reject(proposed surface storage methods) as inadequate’. The solution to the high level waste problem is ‘transcientific’. The critical problem of disposal is that the degree of permanence needed subjects any scheme to geological requirements and the enormous time-span involved reduces the relevance of any empirical data to a low value. There is thus no scientific evidence that vitrified solidified high level wastes in deep geological formations forming a central repository will remain in one piece, be insoluble, or inert over periods considerably shorter than these. Further no responsible geologist can offer a guarantee. The disposal should and must be retrievable, which then also means surveillance over geological time scales far exceeding the period of human experience of observed cultures(Tolstoy 1986,Boyle 1986, Lovins and Price1975).
An idea of the mess the nuclear enterprise has landed itself in can be gleaned from the fact that in the US, the Department of Energy is committed to spending 2.5 billion dollars(about 4000 Cr 1989 Rupees) over the next five year period till 1992 to solve the high level waste disposal problem. A number of states in the US have enacted legislation denying electric utilities the option to build new nuclear power plants until proven disposal techniques are developed(Electrical World, July 1986).
Performance of Indian Nuclear Stations
According to an advertisement supplement in the Times of India dated October 16th 1987, taken out by the Nuclear Power Corporation, the average yearly capacity factor of all the nuclear power plants from 1969 to July 1987(about 18 years) works out to 46.26%. Compare this with the boiling water GE reactor in US(58% for 1968-84 and 51.2% in 83-84) and for Canada:Average lifetime capacity factor 77.1%. The Indian Nuclear performance in the three recent years has been, on the aggregate, 46.27& for 1985-86,46.62 in 1986-87, and 46.67 in 1987-88. Thus if the Indian Nuclear Power Programme, from now on, maintains an average plant (or capacity) factor of 62%, the overall plant factor between 1969 to 2001 AD would be about 53.4%. But the assumption of a jump from a historical 46.47% to 62% on a sustained basis for the plant factor may not be warranted for the same reasons that are ascribed to the programme’s past performance, with some additional ones thrown in, like untried 500 MW designs and probably lack of sufficient heavy water in time, unfamiliar new types of reactors, and, of course, accidents. Thus we may consider a plant factor of 50%an average plant factor till 2001 from now, for purposes of our analysis and see the implications.
Output/Input Ratio for a Plant factor of 50%
With a construction energy input per year for a 1000 MW Candu reactor of 2510 MkWh and an energy output per year corresponding to 50% plant factor and about 11% transmission losses of 3484 MkWh the output per year to input per year ratio would be 1.39. We note that this ratio does not make any allowance for energy required for storage of high level wastes. Thus the output/input ratio for the Indian Nuclear Power programme could easily be less than that indicated for by this analysis. Om account of economies of scale, as far as the construction energy is concerned, units of less than 1000 MW size would have a lower output/input ratio than a 1000 MW reactor. For computing the energy balance of the Indian programme to 2001 AD we shall take a ratio of 1.39 and compare it with other ratios for implications.
Energy Balance for the Indian Nuclear Programme 1985-2001 AD
This energy balance will be carried out on the basis of the capacity build- up data furnished in the supplement issued by the NPC in the newspapers on October 16th, 1987.
As per data published in an NPC supplement in the Times of India dated October 16th 1987, the capacity build-up is as indicated in Table 4. The energy delivered at 62% plant factor and at 50% plant factor is also shown in the Table. It is seen from Table 4 that the energy delivered during the period 1985-2001 AD would for 0.015 w/w% U3O8 ore total 200626 MkWh and for 0.07 w/w% U3O8 ore 216444 MkWh, both at 50% plant factor. In both cases transmission losses are assumed to be 11%. As against this, the energy invested in the construction of theses plants would be (201774+14824) MkWh for 0.015 w/w% U3O8 ore and (194277+14824) MkWh for 0.07 w/w% U3O8 ore. The energy delivered by by these plants at 50% plant factor during 1985-2001 AD would at most therefore equal the heat energy utilised in the construction of these reactors. We should also debit some energy towards maintenance of storage tanks for high level radioactive wastes , against energy delivered during these 17 years. Further we have not considered the construction energy of those reactors which will become operational after 2001 AD, but which willhave to be taken in hand during the period till 2001 AD.
Thus we see that during this period we get no energy at all on balance from these reactors. Just imagine that society would be paying for this electricity, delivered at 85 paise per kWh(1988 prices), some 17900 crores of rupees, or, since the cost of electricity has now become of the order of Re.1/- per kWh, Rs. 21000 Cr(1989 prices) and society will, on balance, have received nothing because the heat energy of high quality withdrawn from society during this period equals the electricity delivered. The net cost to society is therefore infinite per unit energy received during this transaction.
Today the requirements for construction energy for these reactors are met aminly by fossil fuels in India. The major portion of high quality energy required for the construction of nuclear plants is consumed as heat in steel and cement. An idea of the cost of this heat energy can be obtained by a comparison of heat and electricity inputs in the industrial sector in terms of quantity and cost in India. This is brought out in Table 6. Using a conversion factor of 4 for electrical to thermal kilowatthours, the total energy input in the industrial sector per annum from table 6 evaluates to 652865 MkWh(t). The electricity consumption per year 60,000 MkWh(e). Thus the electricity consumption forms 9.19% of the total energy input. The total cost of the other energy inputs-coal and petroleum inputs amounts amounts to 4700 crores of rupees. The corresponding energy consumed being 412865 MkWh. Thus the average cost of coal and petroleum fuel inputs is 11.38 paise per kWh.
Now the cost of electricity from 2*235 MW nuclear reactors according to NPC would be 85 paise per kWh for units commissioned in 1992. This assumes a capital cost of 15405 rupees per kilowatt of installed capacity. But post TMI and post Chernobyl costs would be nearer 2.5 times this amount if the requisite improvements are incorporated which means a cost per unit of electricity delivered of 0.85*2.5=Rs.2.1. If we assume a rise in heat energy cost to, say, 21 paise per kWh, we can expect electricity from a nuclear plant to cost ten times the heat energy cost.
In Table 7, the share of heat and electricity consumptions in the industrial sector is given. The potential for energy conservation in all these is of the order of 20 to 30% only(National Productivity Council, Report on Utilisation and Conservation of Energy, New Delhi, 1983). Thus the nuclear enterprise would consume in these 17 years 1985-2001 AD, high quality cheap heat energy of premium fuels by withdrawing these from society and deliver, during the same period, ten times costlier electricity equal to about the quantum of heat taken away. But as brought out in Table 7 less than 10% of energy requirements of the entire society is in electrical form. What is needed to an extent of 95% at any given period and which was available for say 20 paise per kWh is replaced by something the requirement for which is hardly 5 to 10% and at ten times the cost(Really at infinite real cost according to our finding above!).
Thus the consumer may be led to change over from his simple equipment to devices using electricity alone which would be costlier both as regards equipment as well as electricity charges. And this is done by the nuclear industry by converting nuclear fuels at 28% thermal efficiency. Thus during the 1985-2001 AD period, in the nuclear industry, fuel stocks consumed are 3.57 units nuclear fuel plus one unit fossil fuel in the construction of nuclear facilities, to give back net one unit of electricity, out of which only 0.05 units are required by society. Thus the overall “efficiency” of energy delivered to society is 0.05/(3.57+1.0)=0.0109 or 1.09%. This is for the period 1985-2001 or some three five year plan periods or more.
What are the consequences of such a needless conversion? Neither Table 5 nor Table 7 shows such a massive need for electricity. The result is entirely predictable. State electricity boards like in Sweden and France having created vast surpluses of electricity from fuel, which could have been directly and enormously(in fact infinitely) more efficiently used for producing heat, now subsidise the use of electricity for heating at low temperatures! Thus the path followed is from generation of high quality heat from fossil fuels to build nuclear plants, which output less electricity than the energy used in their construction because of the enormous requirement of energy needed to maintain waste storage devices for infinitely(more than hundred million years) long periods to subsidise immediate use of infinitely costly nuclear electricity to produce low quality heat!
France thus sells its electricity across the channel to surplus electricity Britain which is busy creating more surplus electricity by building nuclear plants which the public do not want! And when there is glut... Look at this report from France(Modern Power Systems, August 1987): EdF has a virtual moratorium on reactor orders and the slow down in orders from EdF has forced Framatome,a nuclear reactor manufacturer, to close down one plant. EdF is the French State electricity board. But in the US market forces and public opinion have found other arrangements for meeting the demand for energy. And Sweden is phasing out its 9435 MW of nuclear electricity capacity by 2010. But in India we are supposed to look forward to the Fast Breeders as a lasting source like France. The potential, for extreme danger, of such lasting sources of untested-for-feasibility reactors, has been vividly brought out by R. E . Webb who made a detailed study of the West German SNR 300 reactor of the fast breeder type and found that it can explode like several Hiroshimas(Webb 1986).
Forests are the perfect way to convert nuclear energy to use, nuclear energy of the most advanced form, viz. fusion in the sun located safely, ecologically appropriately, some 150 million kilometers away from the earth.
References
1. Flavin C.1987. Reassessing Nuclear Power:The Fallout from Chernobyl.pp 18-19. Paper No.75.Worldwatch Institute..Washington D.C., March.
2. Ghosh S.1984. “Development: The Real options”. The Ill. Wkly.Ind. June 24-30, p 43.
3. Issacson R.E and Brownell L.E.1973.”Ultimate Storage of Radioactive Wastes in Terrestrial Environments”. In OECD-NEA/IAEA. Management of Radioactive Wastes from Fuel Reprocessing. OECD 66 73 02 3. p.955. Quoted in Lovins et al (op cit) p.34 and p.85-86.
4. Jagus P.J.1981.Energy Profile of the Indian Cement Industry. In “Workshop on Energy: Paper and Cement Industries”. The Industrial and Credit and Investment Corporation of India Limited, Bombay. Summary Proc. And Papers. p.303.
5. Lovins A.B and Price J.H.1975. Non-nuclear Futures: The Case for an Ethical Energy Strategy. Harper-Colophon Books. Harper & Row, Publishers. Sao Paulo.pp.181-190;pp96-97.
6. Tolstoy.I.1986. “High Level Waste: No Technical Solution”. The Ecologist.Vol.16,No.4/5,pp.205-209. Also Boyle S.(in the same issue).”Nuclear Waste-The Unsolved Problem”.
7. Webb R.E.1986. “Western Reactors: How They Compare With Chernobyl ”. The Ecologist. op cit. Pp.166-167. Also,”The Health Consequences of Chernobyl”. The Ecologist. Op cit. pp.169-170, and The Ecologist. No.6.1986..Vol.16.
TABLES








